如何看待 DeepMind 新发布的 AlphaGeometry?

我对于Q-star的猜想与deepmind的实际研发工作有很多相似之处。

我尝试从比较宏观的角度来看待未来AI数学模型的改进方向（可能比较片面，仅做抛砖引玉的作用）。

在很长时间内数学都被认为人类智商的真正高地，因为里面有着很多思考的过程，而且里面的弯弯绕绕太过于复杂了。

而且无论是写数学题还是证明定理，都需要一个东西叫做灵感。

灵感到底是什么?

我认为可以看作人脑通过过往的数学知识对于最优路径的拟合。

而解答数学题的过程其实就是灵感+遍历。我们产生一个又一个灵感，然后再排除一个又一个灵感，直到找到正确的灵感。

过去的机器证明大量的工作都在为验证做准备。验证是实现灵感的前提，因为只有可以验证，那么我们才可以通过程序来生成大量的题目，从而完成AI的训练。

在可以预期的未来，随着可验证的数学领域的不断扩展和AI的不断强化，未来也许会有有限域证明机器，数论证明机器，流体力学证明机器等等。我可以相信未来AI可以解决一些目前人类难以想象的难题，也许是哥德巴赫猜想，谁知道呢？

但是目前的AI架构和数学领域的发展之间还是有一些不同的，这是我本文想说的东西。

在数学领域中，人们具有抽象的概念，从而提出了许多新的概念，例如群，环，域，椭圆曲线等等。以及将一些有证明过程合理的总结为定理，从而帮助我们简化证明定理。

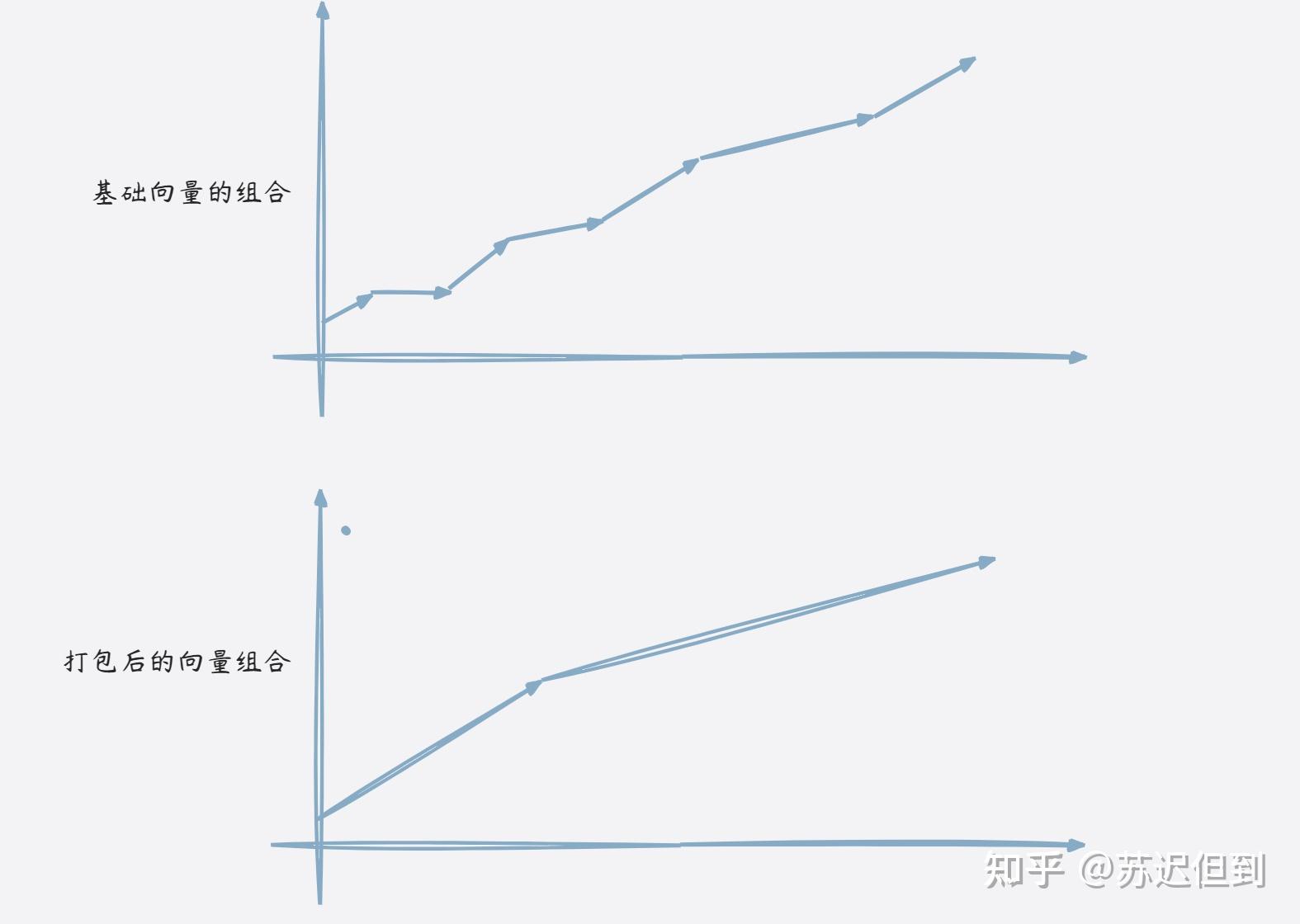
这个简化过程就类似于将一大堆向量简化为了一个新的向量基，从而使得我们可以证明一些非常有难度的问题。不然每一个证明里面的引理都充分展开，就如同print("hello world")一样看上去很简单，但是展开之后的包的体积可能几十M。

但是AI目前还不具备这种抽象能力。

虽然形式上来看，由很多段小的证明和几个分块的证明看上去的效果是一致的。

但是通过引理的方式，可以帮助AI节约路径长度，从而提高效率。

引理应该通过人工导入吗？

虽然在alphago里面会人工导入棋谱，但是alphazero就已经完全重新开始对局了。

在AI里面，越多先验，越意味着上限的限制。虽然在短期，充分的先验有利于帮助它证明更难的一些问题，但是同样也会锁死它的上限。

因此最终还是要让AI学会对证明过程的打包。

让AI学会创建定理并尝试引用自己创建的定理，那么需要重新设计强化学习网络。

一个简单的奖励函数可以设计为当前总共有m个定理，新增了一个定理，可以有效节约1/n的证明步骤。

当1/m>1/n的就可以认为这个定理存在是必要的。

这样的过程可以诱导AI去总结不同情况的共性。

（以上奖励函数仅为随手写的）

虽然从长期来看，抽象思维作为先验的引入可能也会导致AI的水平的下降，但是架构上的先验的效果好处远远大于数据集上的先验好处。