为什么非要用移码而不是原码来比较整数大小?

因为移码是比较数字大小的编程量最小方法。

给你两个原码你要怎么比较大小呢？（注意，这个时候你只有硬件可以使用，既且或非移位）

例如0 1101111和1 0010010，又比如111000和100111

我们来画一个流程图，看看原码比较大小模型下的复杂程度。

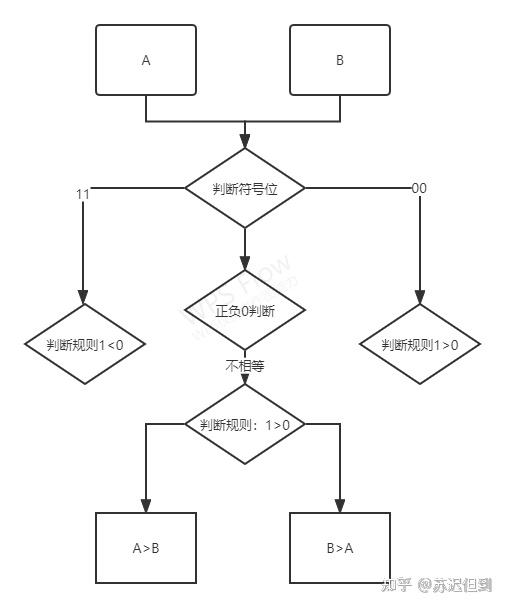
你看要直接比较原码大小这么复杂，因此在比大小的时候往往会使用移码比较。

移码是什么？

移码本质是这个公式： .

.我们小学二年级真的就学过这个公式 。

这个公式帮助我们将数字从 .其中[1,255]都是正数，我们只需要从高位1的出现，就可以快速的判断出大小。

至于小数和整数本质没有区别，小数也可以生成自己的移码。

Tip:移码表示中，0有唯一的编码——1000…00，当出现000…00时（表示－2En），属于浮点数下溢。因此不考虑负0的比较大小问题。

因此我们可以很少的硬件部分就实现了两个数的大小比较，这样才有利于提高速度。

Tips:在IEEE 754当中，阶码也是移码，但是它的偏置值是127，也就是说 。

那如果阶码出现了0或者255会出现什么情况呢？

如果阶码是0的话，符号位是0，则这个数是正0.符号为1的话是负0.

如果阶码是255的话，符号位是0，则这个数是正无穷，符号位是1的话则是负无穷。

引入这两个数字的情况下，是为了计算出现异常情况下，依然将程序继续进行下去。

推荐一本好书，欢迎大家购买。