机器学习的本质是什么？

本文同时适合路人，新手，初学者和有机器学习经验的人。

机器学习的本质是压缩和拟合。

我们将从一个最经典的深度学习算法CNN来简单描述。CNN包括卷积层，池化层，还有全链接层等等其他，请你暂时先不要深究这些名词背后的意思。

我们先来回答这里的拟合到底是什么意思？

在拟合这里，我们要抛弃掉图像的概念。所有的输入的本质是01比特流，或者更形象地来说是1000个0-255的自然数。

如果我们有一个非常大的分布表，那么理论上我们可以将每一种数字组合对应一个输出数字，从而当任意一个数字组合输入的时候，我们都可以快速返回答案。

但是这么做的缺点只有一个，我们这个分布表一共需要 项，那将存储的数据的会比全世界的硬盘总量还要大。

所以有两方面的能力束缚着我们构建一个分布表。

第一方面，存储这么大的分布表所需要的存储空间很大。另外一方面，我们的数据集是有限的，我们压根不能知道绝大多数的数字组合的输出是什么？我们手中即使有1400万张图片，但是在整个数字空间中依然是很小的一部分，微不足道的一部分。

所以我们需要使用一个找到一个方法，让只需要少量的输入和输出对就可以来预测下一个新的输入对。

现在，我们就把这种方法定义为拟合。

我们从简单的拟合开始考虑，在二维图像中，我们假设输出是x，输入是y，我们可以输入 三个点，可以可以设计一个二次函数来很好的拟合三个点。

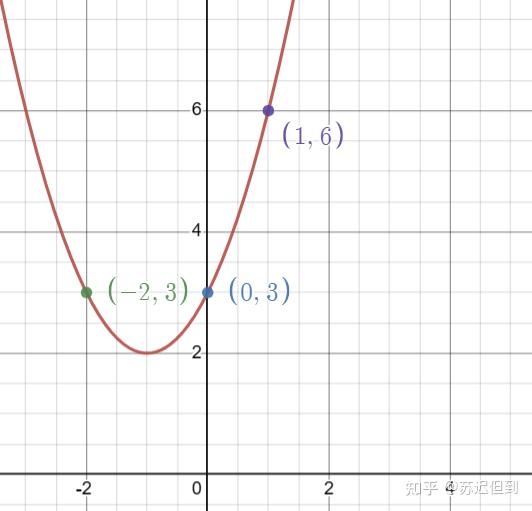
但是有一个问题所在，我们怎么知道第四个点在图像上，万一真实的点分布其实是这样的？

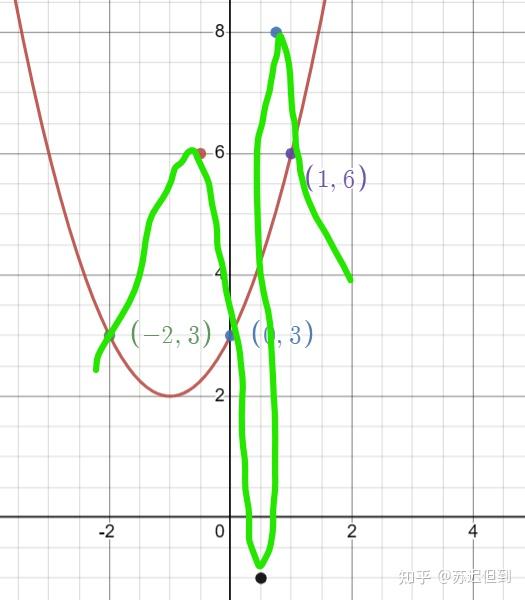
这是因为我们通常假设自然界是连续，且有规律的。改变一个像素点不会导致图片里面的猫变成狗，改变10个也不会，变化是在逐渐进行中的。

所以我们的拟合大多数时候都工作的很好。

一个参数远远不够描述我们的输入情况，在更高的维度中,输入的也许是 .

如果有足够数学基础的话，那么我们可以尝试构造一个函数来满足它。但是我们现在不能手动计算，所以我们预设好一个基础函数，一个复杂的高维曲线。我们通过修改里面的参数来让这个复杂的曲线尽可能的适应已有的数据集。当参数越多的情况下，这个曲线适应的越好。

现在回到为什么要卷积和池化上？

因为我们要控制输入的参数的大小，如果输入的参数量过多，那么相应所需要适应的函数参数也更多。这会导致我们计算变得更加低效，复杂度上升。而且点在空间中过于稀疏的话，那么拟合效果也会很差。

也就是说参数量大小与数据集大小应当相互匹配的。

而数据集大小在很多时候又不是可控的，不能一味的扩大，取决于人力，资金，现实环境等等限制。所以一定情况下的参数量大小固定的情况下，我们需要压缩数据，让它适配参数量大小。

科学家开始着手尝试来直接从图像中提取关键信息。

一个最简单的想法就是我们只需要其中的黑白线条。

然后或者我们不需要那么高的分辨率，4k可以看清楚，其实256*256也可以看清楚。

再然后或许我们可以把图片卷积起来，可以保留一定尺度下的更为重要的信息。

通过这些手段，我们将数据中的一些本质特征保存下来，过滤掉了无关特征。

所以留给我们的问题也出现了。

如何更好的压缩？如何更快更准确的修改参数？